If you like flipping coins, and you like water, and you like contemplating how you might combine those two interests, consider this line of approach:
“Coins falling in water,” Luke Heisinger, Paul K. Newton [pictured here, above]] and Eva Kanso [pictured here, below], Journal of Fluid Mechanics, vol. 742, March 2014, pp. 243-253. (Thanks to investigator Tom Gill for bringing this to our attention.) The authors, at the University of Southern California, Los Angeles, report:
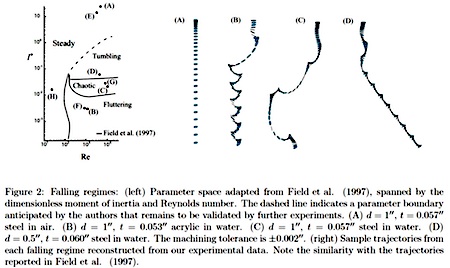
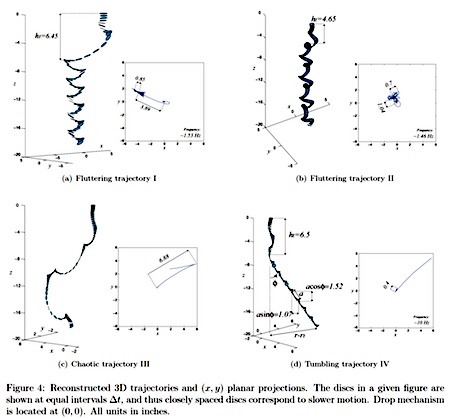
“When a coin falls in water, its trajectory is one of four types, determined by its dimensionless moment of inertia I and Reynolds number Re: (A) steady; (B) fluttering; (C) chaotic; or (D) tumbling. The dynamics induced by the interaction of the water with the surface of the coin, however, makes the exact landing site difficult to predict a priori. Here, we describe a carefully designed experiment in which a coin is dropped repeatedly in water to determine the probability density functions (p.d.f.s) associated with the landing positions for each of the four trajectory types, all of which are radially symmetric about the centre drop-line…. For the steady and fluttering modes, the coin never flips, so the coin lands with the same side up as when it was dropped. The probability of heads or tails is close to 0.5 for the chaotic mode and, in the case of the tumbling mode, the probability of heads or tails is based on the height of the drop which determines whether the coin flips an even or odd number of times during descent.”
A few details from the study:
The study cites several papers by 2007 Ig Nobel physics prize winner Mahadevan. It also cites the classic study: “Dynamical bias in the coin toss,” Persi Diaconis, Susan Holmes, Richard Montgomery, 2007, SIAM Rev., 49, 211-235.