Quantum Gravity Treatment of the Angel Density Problem
[EDITOR'S NOTE: we apologize for the lack of clear formatting,in this web version, of the mathematical formulae.]
Abstract
We derive upper bounds for the density of angels dancing on the point of
a pin. It is dependent on the assumed mass of the angels, with a maximum
number of 8.6766*10exp49 angels at the critical angel mass (3.8807*10exp-34
kg).
Ancient Question, Modern Physics
"How many angels can dance on the head of a pin?" has been a
major theological question since
the Middle Ages.[5]
According to Thomas Aquinas, it is impossible for two distinct causes to
each be the immediate cause of one and the same thing. An angel is a good
example of such a cause. Thus two angels cannot occupy the same space.[2]
This can be seen as an early statement of the Pauli
exclusion principle. (The Pauli exclusion principle is a pillar of modern
physics. It was first stated in the twentieth century, by Pauli.)
However, this does not place any upper bound on the density of angels in
a small area, because the size r of angels remains undefined and could possibly
be arbitrarily small. There have also been theological criticisms of any
assumption of angels as complete causes.
Stating the Question Correctly
The basic issue is the maximal density of active angels in a small volume.
It should be noted that the original formulation of the problem did not
refer to the head of a pin (R¼1 mm) but to the point of the pin. Therefore,
the point, not the head, of the pin is the region that will be studied in
this paper.
One of the first reported attempts at a quantum gravity treatment of the
angel density problem that also included the correct end of the pin was
made by Dr.
Phil Schewe. He suggested that due to quantum gravity space is likely
not infinitely divisible beyond the Planck length scale of 10exp-35 meters.
Hence, assuming the point of the pin to be one Ångström across
(the size of a scanning tunnelling microscope tip) this would produce a
maximal number of angels on the order of 1050 since they would not have
more places to fill.[1]
While this approach does produce an upper bound on the possible density of angels, it is based on the Thomist assumption of non-overlap.
Since angels can be presumed to obey quantum rules when packed at quantum
gravity densities, the uncertainty relation will cause their wave functions
to overlap significantly even if there is a strong degeneracy pressure.
If the non-overlap assumption is relaxed, this approach cannot derive an
upper bound.
Quantum
Gravitational Treatment
A stricter bound based on information physics can be derived that is not
based on overlap assumptions, but merely the localisation of angelic information.
Assuming that each angel contains at least one bit of information (fallen
/ not fallen), and that the point of the pin is a sphere of diameter of
an Ångström (R=10exp-10 m) and has a total mass of M=9.5*10exp-29
kilograms (equivalent to that of one iron atom), we can use the Bekenstein
bound[3] on information to calculate an upper bound on the angel density.
In a system of diameter D and mass M, less than kDM distinguishable bits
can exist, where k=2.57686*10exp43 bits/meter kg.[7] This gives us a bound
of just 2.448*10exp5 angels, far below the Schewe bound.
Note that this does not take the mass of angels into account. A finite
angel mass-energy would increase the possible information density significantly.
If each angel has a mass m, then the Bekenstein bound gives us N<kD(M+Nm).
Beyond mcrit>1/kD ¼3.8807*10exp-34 kg this produces an unbounded maximal
angel density as each angel contributes enough mass-energy to allow the
information of an extra angel to move in, and so on.
However, if angels have mass, then the point of the pin will collapse into
a black hole if c2R/2G< Nm (here I ignore the mass of the iron atom at
the tip).4 For angels of human weight (80 kg), we get a limit of 4.2089*10exp14
angels. The maximal mass of any angel amenable to dance on the pin is 3.3671*10exp16
kg; at this point there is only room for a single angel.
The picture that emerges is that, for low angel masses, the number is bounded
by the Bekenstein bound, and increases hyperbolically as mcrit is approached.
However, the black hole bound decreases and the two bounds cross at mmax=1/(4GkM/cexp2+kD),
very slightly below mcrit. This corresponds to the maximal angel density
of Nmax=8.6766*10exp49 angels (see figure).
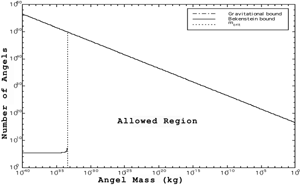
Maximum number of angels for a given mass. The allowed region is bounded from above by the line c2R/2G=Nm (gravitational collapse) and the curve N=kD(M+Nm) (information density) which has an asymptote for mcrit, and from below by N=0. The maximal number of angels occurs at the intersection of the gravitational bound and the asymptote at mcrit
Dance Dynamics
If the angels dance very quickly and in the same direction, then the angular
momentum could lead to a situation like the extremal Kerr metric, where
no event horizon forms (this could also be achieved by charging the angels).[4]
Hence the number of dancing angels that can crowd together is likely much
higher than the number of stationary angels.
However, at these speeds the friction caused by their interaction with
the pin is likely to vaporise it or at least break it apart. Even for a
modest speed of 1 m/s the total kinetic energy of Nmax angels of mass mcrit
would be 1.682*10exp16 J. In the case of charged angels at relativistic
densities, pair-creation in their vicinity would likely cause the charge
to dissipate over time,6 and charge transfer to the pin would also likely
induce electromechanical forces beyond any material tolerances.
The uncertainty relation also imposes a limitation on the dance. Since
the uncertainty in position of the angels by assumption is less than the
size of the point ŠxR we find that the uncertainty in momentum must be
Šphbar/R, and this leads to a velocity uncertainty Šv>hbar/Rm. If m=
mcrit we get Šv>> 8.6766*10exp59 m/s (>> c), which shows that:
(1) the angels must dance with speeds near the velocity of light in order
to obey quantum mechanics;
(2) a full relativistic treatment is necessary; and
(3) that the precision of the dance must break down due to quantum effects.
This can be used to rule out certain types of dance due to their high precision
requirements.
Discussion
We have derived quantum gravity bounds on the number of angels that can
dance on the tip of a needle as a function of the mass of the angels. The
maximal number of angels -- 8.6766*10exp49 -- is achieved near the critical
mass mcrit>1/kD ¼3.8807*10-34 kg, corresponding to the transition from
the information-limited to the mass-limited regime. It is interesting to
note that this is of the same order of magnitude as the Schewe bound.
Angel physics has until now mainly employed theological methods, but as
this paper shows, modern information physics, quantum gravity and relativity
theory provide powerful tools for exploring the dynamics and statics of
angels.
These bounds are only upper bounds, and do not take into account the effects
of a finite number of available angels, degeneracy pressures if angels obey
the Pauli exclusion principle as suggested by Aquinas, or the theo-psychology
of the angels themselves. The exact dance dynamics also clearly play a major
role. A full relativistic treatment of the dance appears as a promising
avenue for further tightening of the bounds.
Bibliography
1. Reported in the New York Times, November 11, 1997, "Science
Q \& A: Dancing Angels," by C. Claiborne Ray <http://www.nytimes.com/learning/students/scienceqa/archive/971111.html>.
Dr. Phil Schewe presented his idea at a meeting of the Society for Literature
and Science in 1995. It should be noted that the given density in the New
York Times is wrong, as it did not count the area, just the length.
2. T. Aquinas, Summa Theologiae, vol. 52, no. 3, 1266.
3. J. Bekenstein, Physical Review D, vol. 23, no. 287, 1981.
4. Gravitation, C. Misner, K. Thorne, and J. Wheeler, W.H. Freeman
and Co., 1973.
5. Memoirs of the Extraordinary Life, Works and Discoveries of Martinus
Scriblerus, 1741, A. Pope, J. Swift, J. Gay, T. Parnell, and J. Arbuthnot,
ed. by C. Kerby-Miller, 1950; republished 1966.
6. "On the Dyadosphere of Black Holes," R. Ruffini, in Proceedings
of Yamada Conference, Kyoto, Japan, April 1998. <http://xxx.lanl.gov/abs/astro-ph/9811232>.
7. The Physics of Immortality, Frank Tipler,. Macmillan, London,
1994.
© Copyright 2001 Annals of Improbable Research (AIR)
This HotAIR feature first appeared in VOLUME
7-ISSUE 3 of the print magazine. For a complete list of web site featured
articles, see What's New.